translation of axes
The shifting of the reference axes without turning so that each axis remains parallel to its original position. Once the origin O of a system of x- and y-axes is shifted to the point O´(xo, yo) in the original system, each point p(x, y) in the original system needs to be given a new set of coordinates p´(x´, y´) in the new system according to the following relationships:

symbol spacex = x´ + xo
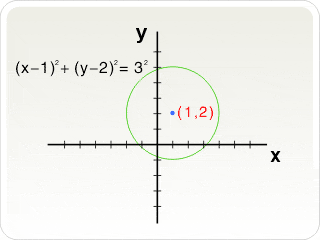
symbol spacey = y´ + yo

The purpose of such an axes translation is to simplify the equation of a curve for further processing. For example, a circle with a center at (1, 2) and a radius r = 3 can be described by the following equation:

symbol space(x - 1)2 + (y - 2)2 = 32

When the reference axes are shifted to O´(1, 2), the same circle can be described:

symbol space[(x´+1) - 1]2 + [(y´+2) - 2]2 = 32
or
symbol space(x´)2 + (y´)2 = 32

As shown, the equation in the new system is definitely easier to work with.

Related Term: rotation of axes


 
English | Espaņol